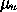Answers to Part 2 - An Increase in the Diluent Flowrate

Question 1

How does the system respond with no control?

At the initial conditions the flowrates of both diluent and concentrate are 1.0 units/time. Hence the concentration of concentrate starts at 0.5.

However at the final steady state conditions the flow of diluent increases to 1.5 and so the concentration of concentrate decreases to 0.4.

Question 2

How quick is the response?

The time constant can be evaluated to be 0.667 and the system takes approximately 4/5 time units to reach steady state.

Question 3

Is the controller gain +ve or -ve?

We have already shown that when the concentrate flow increases the concentrate increases and so the controller gain will be +ve.

Question 4

• What is the smallest gain which gives a constant amplitude oscillation (the ultimate gain)?
• What is the period of this oscillation?
• What controller settings does this give (ZN closed-loop method)?

This question is looking at a tuning method called the Zeiglar Nichols Closed Loop Response Method. In this procedure it is necessary to run the process with proportional only control and find the point where the system starts oscillating with constant amplitude. This gives values for the ultimate gain (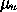) and the ultimate period of oscillation (Pu).

Then substitute into the following equations to obtain the tuning parameters:

Gain = 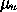/2 for proportional only control

Gain = 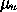/2.2 and Reset Time = Pu/1.2 for PI control

In this example 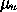= 14 and Pu = 1.8

Therefore:

• Proportional Controller Gain = 7
• PI Controller Gain = 6.36
• PI Controller Reset = 1.5

Question 5

At gains below 14 the response is damped but at gains above 14 the response stays constant as opposed to oscillating out of control. The reason for this is that the concentrate flow is kept within the limits of 0 - 1.6 and it is hitting these limits each time.

Question 6

• Compare the two ZN tuning methods
• What controller settings give the best response?

For a PI Controller:

• ZN Open Loop Method gives: Gain of 6 and Reset Time of 1.65
• ZN Closed Loop Method gives: Gain of 6.36 and Reset Time of 1.5

Both of these are very similar. However a slightly better response is acheived if a Gain of 5 and Reset Time of 1 is used.

Please move Back to the previous page