The Mixing Process

Aims of Experiment

• To appreciate the difficulties in trying to tune a controller for a real process
• To compare the ZN open loop and closed loop methods for tuning a controller

Theory

However it is advisable to work through the other tuning experiments before tackling this one,

• Introduction to Zeigler Nichols Tuning Methods
• Further Examples in Open Loop Tuning
• Further Examples in Closed Loop Tuning

Experimental Apparatus

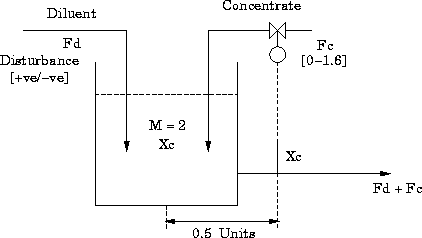
As can be seen there are two streams, a diluent and a concentrate, mixing together in a tank. The aim is to keep the concentration of concentrate constant by manipulating the flowrate of the concentrate stream. The system is disturbed by altering the diluent flowrate.

Some notes on the system are listed below:

• The mass in the tank stays constant at 2 units, i.e. the flowrate into the tank is the same as what comes out.
• The equations which model the system assume perfect mixing
• The measured/controlled variable is the concentration of the concentrate in the tank.
• The measurement of this concentration is delayed by 0.5 time units.
• The adjusted variable is the flowrate of concentrate into the tank. This value is limited to the range 0 - 1.6 mass units/time unit.
• The disturbance is the flow of diluent into the tank.

Procedure

• No disturbance
• An increase in the diluent flowrate
• A decrease in the diluent flowrate

Since it is non-linear the response of the system to each of these cases will be different. The important thing to understand from this experiment is that the tuning parameters therefore, will also be different.

For the first part it is a matter of looking at the response and saying what it tells you about the process. For the second and third parts it is necessary to look at the effect of the disturbance and try different control parameters to return the process to its original state. To do this simply enter the new values for the gain and reset time and Rerun Simulation

Please move on to Pre-Experimental Questions